Of all of James Grigsby's productions, whether it is with the Motor Totemist Guild or, Strange Attractors is the work he will be remembered for. This album, weaved on a complex story line jumping back and forth from 1957 to 1985 to 2012, contains some of the best music avant-prog had to offer in 1990s. The lineup for this album is mostly Sanjay Kumar (keyboards), David Kerman (drums), Eric Johnson (bassoon), Emily Hay (flute, singing), Steve Cade (guitar), and Grigsby (guitar, bass, computer, tapes), with a few guests. The music takes the complexity and symphonic side of Canterbury progressive rock and perverts it in a Henry Cow meets kind of way, blending into it free improv and atonal classical music elements.
Although very complex and hard to get into, Strange Attractors remains a rock record (unlike some of 's later works). The playing is stellar, surprises abound, the more avant-gardist pieces ('Daikon Batake') being balanced by high-octane prog rock numbers ('No Mo Ippon').
'Ginger Tea' and 'Another Ginger Tea' are two of the most accomplished pieces of progressive rock's most avant-gardist ensembles, turning this album into a classic. ~ François Couture.
Directed by Joe Harris. With Andrew Sensenig, Matt Socia, Craig Cole, Selase Botchway. When two parallel universes, years apart, collide at a certain point in time. In the past, perhaps especially at the end of the nineteenth century and the beginning of the twentieth, most* scientists assumed that provided you knew the 'laws' that governed some system (such as planets orbiting a star, or billiard balls colliding on a table) and knew its state at some initial point that you would be able to. Mar 26, 2013. I wanted to create a series of pictures representing mathematical shapes on white background, like a 'tribute to mathematics' that I often use in my work. I chose the 'strange attractors' for their dynamic forms and 'chaotic feel'. Because I'm not a mathe. Motivation of attractors. A dynamical system is generally described by one or more differential or difference equations. The equations of a given dynamical system.
Visual representation of a strange attractor In the field of, an attractor is a set of numerical values toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed. In finite-dimensional systems, the evolving variable may be represented as an n-dimensional. The attractor is a region in.

In, the n dimensions may be, for example, two or three positional coordinates for each of one or more physical entities; in, they may be separate variables such as the and the. If the evolving variable is two- or three-dimensional, the attractor of the dynamic process can be represented in two or three dimensions, (as for example in the three-dimensional case depicted to the right). An attractor can be a, a finite set of points, a, a, or even a complicated set with a structure known as a strange attractor (see below). If the variable is a, the attractor is a subset of the real number line. Describing the attractors of chaotic dynamical systems has been one of the achievements of.

A of the dynamical system in the attractor does not have to satisfy any special constraints except for remaining on the attractor, forward in time. The trajectory may be. If a set of points is periodic or chaotic, but the flow in the neighborhood is away from the set, the set is not an attractor, but instead is called a repeller (or repellor). Contents • • • • • • • • • • • • • • • • • • Motivation of attractors [ ] A is generally described by one or more. The equations of a given dynamical system specify its behavior over any given short period of time.
To determine the system's behavior for a longer period, it is often necessary to the equations, either through analytical means or through, often with the aid of computers. Dynamical systems in the physical world tend to arise from systems: if it were not for some driving force, the motion would cease. (Dissipation may come from,, or loss of material, among many causes.) The dissipation and the driving force tend to balance, killing off initial transients and settle the system into its typical behavior. The subset of the of the dynamical system corresponding to the typical behavior is the attractor, also known as the attracting section or attractee.
Invariant sets and are similar to the attractor concept. An invariant set is a set that evolves to itself under the dynamics. Attractors may contain invariant sets. A limit set is a set of points such that there exists some initial state that ends up arbitrarily close to the limit set (i.e. To each point of the set) as time goes to infinity. Attractors are limit sets, but not all limit sets are attractors: It is possible to have some points of a system converge to a limit set, but different points when perturbed slightly off the limit set may get knocked off and never return to the vicinity of the limit set. For example, the has two invariant points: the point x 0 of minimum height and the point x 1 of maximum height.
The point x 0 is also a limit set, as trajectories converge to it; the point x 1 is not a limit set. Because of the dissipation due to air resistance, the point x 0 is also an attractor. If there was no dissipation, x 0 would not be an attractor. Aristotle believed that objects moved only as long as they were pushed, which is an early formulation of a dissipative attractor.
Exponential complicates detailed predictions, but the world is knowable due to the existence of robust attractors. Mathematical definition [ ] Let t represent time and let f( t, •) be a function which specifies the dynamics of the system.
That is, if a is a point in an n-dimensional phase space, representing the initial state of the system, then f(0, a) = a and, for a positive value of t, f( t, a) is the result of the evolution of this state after t units of time. For example, if the system describes the evolution of a free particle in one dimension then the phase space is the plane R 2 with coordinates ( x, v), where x is the position of the particle, v is its velocity, a = ( x, v), and the evolution is given. Weakly attracting fixed point for a complex number evolving according to a. The phase space is the horizontal complex plane; the vertical axis measures the frequency with which points in the complex plane are visited. The point in the complex plane directly below the peak frequency is the fixed point attractor. A of a function or transformation is a point that is mapped to itself by the function or transformation. If we regard the evolution of a dynamical system as a series of transformations, then there may or may not be a point which remains fixed under each transformation.
The final state that a dynamical system evolves towards corresponds to an attracting fixed point of the evolution function for that system, such as the center bottom position of a, the level and flat water line of sloshing water in a glass, or the bottom center of a bowl contain a rolling marble. But the fixed point(s) of a dynamic system is not necessarily an attractor of the system. For example, if the bowl containing a rolling marble was inverted and the marble was balanced on top of the bowl, the center bottom (now top) of the bowl is a fixed state, but not an attractor. This is equivalent to the difference between. In the case of a marble on top of an inverted bowl (a hill), that point at the top of the bowl (hill) is a fixed point (equilibrium), but not an attractor (stable equilibrium). In addition, physical dynamic systems with at least one fixed point invariably have multiple fixed points and attractors due to the reality of dynamics in the physical world, including the of,,, (both and ), and even. In the case of a marble on top of an inverted bowl, even if the bowl seems perfectly, and the marble's shape, are both much more complex surfaces when examined under a microscope, and their or during contact.
Any physical surface can be seen to have a rough terrain of multiple peaks, valleys, saddle points, ridges, ravines, and plains. There are many points in this surface terrain (and the dynamic system of a similarly rough marble rolling around on this microscopic terrain) that are considered or fixed points, some of which are categorized as attractors. Finite number of points [ ] In a system, an attractor can take the form of a finite number of points that are visited in sequence. Each of these points is called a. This is illustrated by the, which depending on its specific parameter value can have an attractor consisting of 2 n points, 3×2 n points, etc., for any value of n. Limit cycle [ ]. : an attracting limit cycle Limit torus [ ] There may be more than one frequency in the periodic trajectory of the system through the state of a limit cycle.
For example, in physics, one frequency may dictate the rate at which a planet orbits a star while a second frequency describes the oscillations in the distance between the two bodies. If two of these frequencies form an (i.e. They are ), the trajectory is no longer closed, and the limit cycle becomes a limit. This kind of attractor is called an N t-torus if there are N t incommensurate frequencies. For example, here is a 2-torus: A time series corresponding to this attractor is a series: A discretely sampled sum of N t periodic functions (not necessarily waves) with incommensurate frequencies. Such a time series does not have a strict periodicity, but its still consists only of sharp lines. Strange attractor [ ].
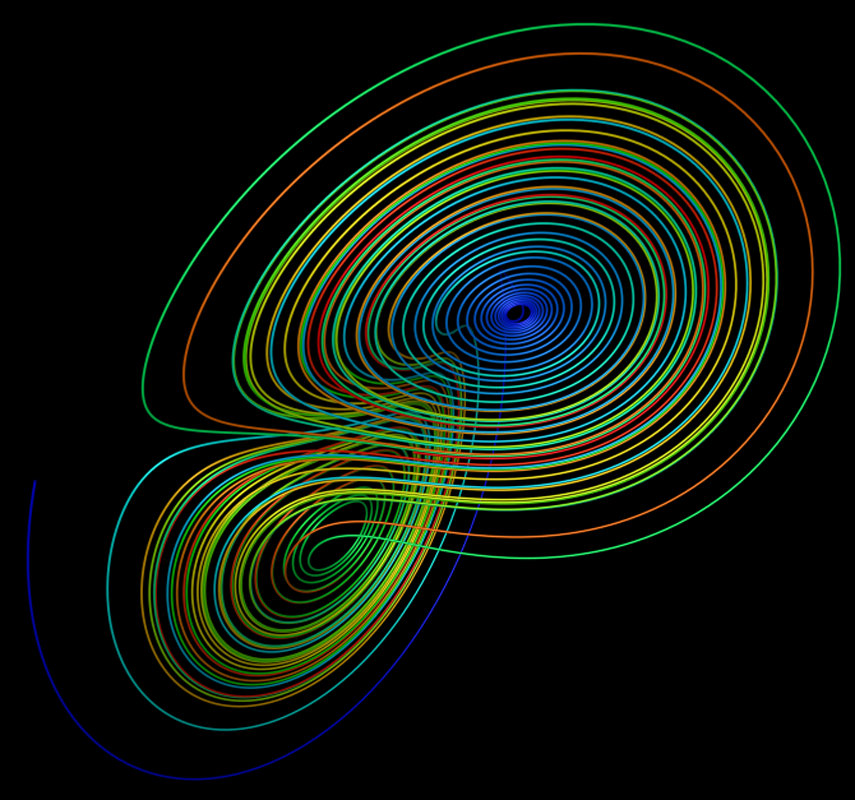
A plot of Lorenz's strange attractor for values ρ = 28, σ = 10, β = 8/3 An attractor is called strange if it has a structure. This is often the case when the dynamics on it are, but also exist. If a strange attractor is chaotic, exhibiting, then any two arbitrarily close alternative initial points on the attractor, after any of various numbers of iterations, will lead to points that are arbitrarily far apart (subject to the confines of the attractor), and after any of various other numbers of iterations will lead to points that are arbitrarily close together. Thus a dynamic system with a chaotic attractor is locally unstable yet globally stable: once some sequences have entered the attractor, nearby points diverge from one another but never depart from the attractor.
The term strange attractor was coined by and to describe the attractor resulting from a series of of a system describing fluid flow. Strange attractors are often in a few directions, but some are a, and therefore not differentiable. Strange attractors may also be found in the presence of noise, where they may be shown to support invariant random probability measures of Sinai–Ruelle–Bowen type. Examples of strange attractors include the,,, Tamari attractor, and the. Effect of parameters on the attractor [ ]. Basins of attraction in the complex plane for using Newton's method to solve x 5 − 1 = 0. Points in like-colored regions map to the same root; darker means more iterations are needed to converge.
2.35287527 converges to 4; 2.35284172 converges to −3; 2.35283735 converges to 4; 2.352836327 converges to −3; 2.352836323 converges to 1. Newton's method can also be applied to to find their roots. Each root has a basin of attraction in the; these basins can be mapped as in the image shown. As can be seen, the combined basin of attraction for a particular root can have many disconnected regions.
For many complex functions, the boundaries of the basins of attraction are. Partial differential equations [ ] may have finite-dimensional attractors. The diffusive part of the equation damps higher frequencies and in some cases leads to a global attractor. The Ginzburg–Landau, the Kuramoto–Sivashinsky, and the two-dimensional, forced are all known to have global attractors of finite dimension. For the three-dimensional, incompressible Navier–Stokes equation with periodic, if it has a global attractor, then this attractor will be of finite dimensions. Numerical localization (visualization) of attractors: self-excited and hidden attractors [ ].
Chaotic (green domain) in. Trajectories with initial data in a neighborhood of two saddle points (blue) tend (red arrow) to infinity or tend (black arrow) to stable zero equilibrium point (orange). From a computational point of view, attractors can be naturally regarded as self-excited attractors. Self-excited attractors can be localized numerically by standard computational procedures, in which after a transient sequence, a trajectory starting from a point on an unstable manifold in a small neighborhood of an unstable equilibrium reaches an attractor (like classical attractors in the,,, and many other dynamical systems). In contrast, the basin of attraction of a does not contain neighborhoods of equilibria, so the cannot be localized by standard computational procedures. See also [ ] Wikimedia Commons has media related to. • • • • • • • • References [ ].
• ^ Boeing, G. Retrieved 2016-12-02. 'On the Concept of Attractor.' Phys 99: 177–195.
• Greenwood, J. Williamson (6 December 1966).. Proceedings of the Royal Society. 295 (1442): 300–319.:. Retrieved 31 March 2013. • Vorberger, T. Department of Commerce, National Institute of Standards (NIST).
• Grebogi, Celso, Edward Ott, and James A. 'Chaos, Strange Attractors, and Fractal Basin Boundaries in Nonlinear Dynamics.' Science 238, no. 4827 (1987): 632–638. • Ruelle, David; Takens, Floris (1971).. Communications in Mathematical Physics.
20 (3): 167–192.. • Chekroun M. D.; Simonnet E. 'Stochastic climate dynamics: Random attractors and time-dependent invariant measures'. 240 (21): 1685–1700.. • Strelioff, C.; HUbler, A.
'Medium-Term Prediction of Chaos'. • Dence, Thomas, 'Cubics, chaos and Newton's method', 81, November 1997, 403–408. • Leonov G.A.; Vagaitsev V.I.; Kuznetsov N.V. Physics Letters A. 375 (23): 2230–2233..
• Bragin V.O.; Vagaitsev V.I.; Kuznetsov N.V.; Leonov G.A. Journal of Computer and Systems Sciences International. 50 (5): 511–543.. • Leonov G.A.; Vagaitsev V.I.; Kuznetsov N.V. 241 (18): 1482–1486..
• Leonov G.A.; Kuznetsov N.V. International Journal of Bifurcation and Chaos. Further reading [ ] • (ed.)... 'On the nature of turbulence'.
Communications of Mathematical Physics. 20 (3): 167–192.. Ruelle (1981). 'Small random perturbations of dynamical systems and the definition of attractors'. Communications of Mathematical Physics.
82: 137–151.. 'On the concept of attractor'. Communications of Mathematical Physics. 99 (2): 177–195.. • David Ruelle (1989). Elements of Differentiable Dynamics and Bifurcation Theory.
Academic Press.. • (August 2006). 53 (7): 764–765. Retrieved 16 January 2008. • Grebogi; Ott; Pelikan; Yorke (1984). 'Strange attractors that are not chaotic'. 13: 261–268..
• Chekroun, M. 'Stochastic climate dynamics: Random attractors and time-dependent invariant measures'.
240 (21): 1685–1700.. • (1996) The Essence of Chaos • (1988) Chaos: Making a New Science External links [ ] • • • Chua's circuit simulation • • • and • • •.
